This article is limited to and based on where my research was at the end of 2017. Since that I have made new findings, which are not documented yet and I have changed the numbering system of patterns.
##Introduction
Polygonal tessellations create interesting and fascinating patterns. These tessellations (tilings) are used in architecture, textiles, board games and many other applications for practical, structural and decorative purposes.
To keep this article short I’m using only honeycomb tessellation and hexagons.
By pattern continuation I mean pattern, usually a color, which continues from tile to tile creating bigger pattern. This picture a good example based on shape by Neil Katz (Inside Smart Geometry 2013).

In this article I’m using only symmetrical edges, so any polygon can connect smoothly to any other polygon. Symmetrical edges means that every edge of the polygon is similar and symmetrical.
In the example in the introduction the hexagon had symmetrical edges. I name these edges “ABA” according to the colours of one edge. Listing the colour of every edge of a hexagon would be “ABA-ABA-ABA-ABA-ABA-ABA”, where “-“ is the corner.
##Hexagon with symmetrical edges
There are 28 different ”ABA” topologies for hexagon. If forking is allowed, but dead-ends not, only five topologies for hexagons. Without forking and dead-ends there are only two different topologies.
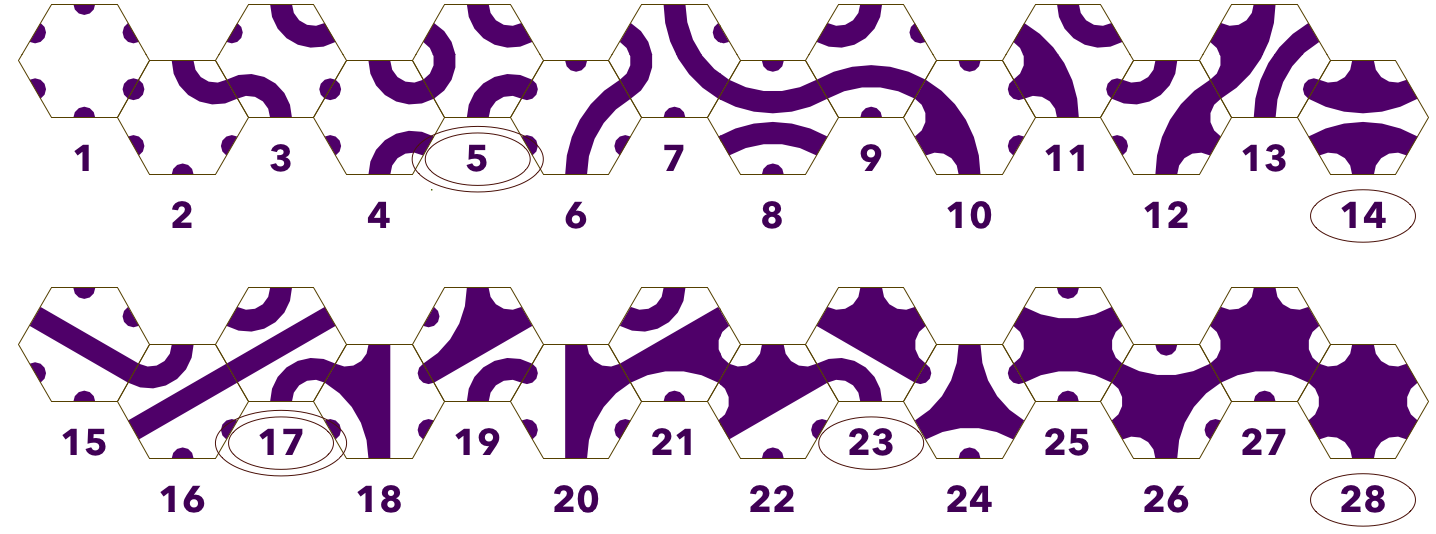
These hexagons can be rotated in six rotations, but some of them appear similar in different rotations.

In this animation different ABA shapes (topologies) are gone through from 1 to 28. Their rotation is from 1 to 6 from left to right except in middle where rotation is random. At the end of the movie both shape and rotation are random.
##ABCBA
“ABCBA” type of edge behaves like “ABA” in two layers. The inner or top shape just must fit inside outer or bottom shape. I call outer or bottom shape as master shape and inner or top shape as sub shape. We get 255 different ABCBA hexagons.

In this animation different ABA shapes (topologies) are gone through from 1 to 28. Their rotation is from 1 to 6 from left to right except in the vertical middle where rotation is random. Lower half is ABA hexagons and upper half is ABCBA hexagons. Inner shape of ABCBA hexagons is always random. At the end of the movie both shape and rotation are random. ##Next
The more I’m playing with these hexagons and other polygons, the more I find new logics, possibilities. My latest findings mean that I have to reprogram my polygon, so it could visualize all ideas.
All graphics are done with ArchiCAD and the base polygon is a GDL program. I’m looking forward to control these GDL objects from Grasshopper.
